La Notation Siteswap (Concepts Avancés) (10/20)
Article proposé par Frédéric Roudaut
Le 15/11/2015.
| ❮ | ❯ |
X - Siteswaps Duaux
La Dualité d'un Siteswap est une propriété mathématique, difficilement palpable jonglistiquement mais qui s'avère intéressante pour générer de nouveaux Siteswaps. Comme on le verra au sein de ce chapitre on retrouve cette notion dans les familles de Siteswaps Vanilles et Multiplexes.
X-1 - Notation Vanille
Tout part d'une curieuse constatation. En effet si on revient sur les tableaux répertoriant le nombre d'états et de transitions des diagrammes Etats/Transitions Vanilles du Chapitre V-1 on constate que pour une même hauteur maximum on retrouve pour 2 valeurs d'objets le même nombre d'états et de transitions. C'est un résultat légèrement contre-intuitif; on s'attendrait à ce que plus y ait d'objets et plus le nombre d'états et de transitions est important. C'est en fait vrai jusqu'à un certain nombre d'objets et ensuite ça décroit. Bien entendu on retrouve cette propriété au sein des diagrammes Etats/Transitions Vanilles réduits.
| Hauteur Max Siteswap | |||||||||||||||||
| Etats Vanilles |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f | |
| Nombre d'objets | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
| 2 | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 66 | 78 | 91 | 105 | |||
| 3 | 1 | 4 | 10 | 20 | 35 | 56 | 84 | 120 | 165 | 220 | 286 | 364 | 455 | ||||
| 4 | 1 | 5 | 15 | 35 | 70 | 126 | 210 | 330 | 495 | 715 | 1001 | 1365 | |||||
| 5 | 1 | 6 | 21 | 56 | 126 | 252 | 462 | 792 | 1287 | 2002 | 3003 | ||||||
| 6 | 1 | 7 | 28 | 84 | 210 | 462 | 924 | 1716 | 3003 | 5005 | |||||||
| 7 | 1 | 8 | 36 | 120 | 330 | 792 | 1716 | 3432 | 6435 | ||||||||
| 8 | 1 | 9 | 45 | 165 | 495 | 1287 | 3003 | 6435 | |||||||||
| 9 | 1 | 10 | 55 | 220 | 715 | 2002 | 5005 | ||||||||||
| 10 | 1 | 11 | 66 | 286 | 1001 | 3003 | |||||||||||
| 11 | 1 | 12 | 78 | 364 | 1365 | ||||||||||||
| 12 | 1 | 13 | 91 | 455 | |||||||||||||
| 13 | 1 | 14 | 105 | ||||||||||||||
| 14 | 1 | 15 | |||||||||||||||
| 15 | 1 | ||||||||||||||||
| -1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | ||
| Somme (0..15) |
0 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | |
| Hauteur Max Siteswap | |||||||||||||||||
| Transitions Vanilles |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | f | |
| Nombre d'objets | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | ||
| 2 | 1 | 5 | 12 | 22 | 35 | 51 | 70 | 92 | 117 | 145 | 176 | 210 | 247 | 287 | |||
| 3 | 1 | 7 | 22 | 50 | 95 | 161 | 252 | 372 | 525 | 715 | 946 | 1222 | 1547 | ||||
| 4 | 1 | 9 | 35 | 95 | 210 | 406 | 714 | 1170 | 1815 | 2695 | 3861 | 5369 | |||||
| 5 | 1 | 11 | 51 | 161 | 406 | 882 | 1722 | 3102 | 5247 | 8437 | 13013 | ||||||
| 6 | 1 | 13 | 70 | 252 | 714 | 1722 | 3696 | 7260 | 13299 | 23023 | |||||||
| 7 | 1 | 15 | 92 | 372 | 1170 | 3102 | 7260 | 15444 | 30459 | ||||||||
| 8 | 1 | 17 | 117 | 525 | 1815 | 5247 | 13299 | 30459 | |||||||||
| 9 | 1 | 19 | 145 | 715 | 2695 | 8437 | 23023 | ||||||||||
| 10 | 1 | 21 | 176 | 946 | 3861 | 13013 | |||||||||||
| 11 | 1 | 23 | 210 | 1222 | 5369 | ||||||||||||
| 12 | 1 | 25 | 247 | 1547 | |||||||||||||
| 13 | 1 | 27 | 287 | ||||||||||||||
| 14 | 1 | 29 | |||||||||||||||
| 15 | 1 | ||||||||||||||||
| -1 | 4 | 9 | 20 | 44 | 96 | 208 | 448 | 960 | 2048 | 4352 | 9216 | 19456 | 40960 | 86016 | 180134 | ||
| Somme (0..15) |
0 | 2 | 5 | 12 | 28 | 64 | 144 | 320 | 704 | 1536 | 3328 | 7168 | 15360 | 32768 | 69632 | 147366 | |
Par exemple pour une hauteur maximum de 5, on a pour 2 et 3 objets, 10 états et 22 transitions. Reprenons donc cet exemple en traçant les diagrammes Etats/Transitions associés sous une représentation graphique équivalente.
Pour une hauteur maximum de 5, le diagramme Etats/Transitions Vanille de 2 objets est le suivant:
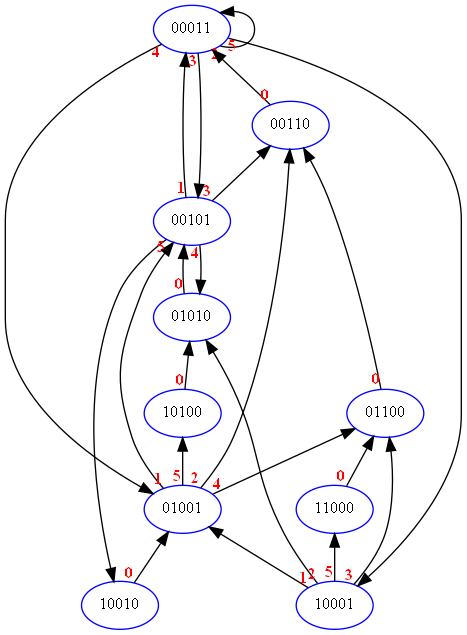
Pour une hauteur maximum de 5, le diagramme Etats/Transitions Vanille de 3 objets est le suivant:
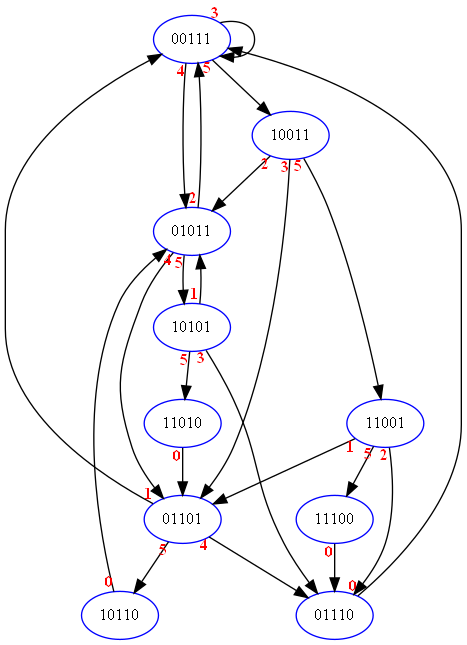
On peut donc superposer exactement nos 2 diagrammes. Pour une hauteur maximum de 5, chaque Siteswap à 2 objets aura donc son Dual à 3 objets. On peut généraliser cette constatation:
tout Siteswap de B objets a un Dual à (H-B) objets.
Pour une hauteur 7, on retrouve bien autant d'Etats et de Transitions à 5 objets qu'à (7-5)=2 objets.
Des 2 précédents diagrammes on en déduit aisément que:
- Un état Dual se déduit en réalisant un complément à 1 d'un état et en inversant ce résultat.
- Une transition Duale se déduit en inversant le sens de la transition et sa valeur devient alors (H-Vk), Vk étant la valeur courante, et H la hauteur maximum.
Pour déduire un Siteswap Dual, il suffit donc de reprendre ces opérations:
Si on s'intéresse par exemple à 97531 à 5 objets et en considérant une hauteur maximum de 9, le Dual associé a (9-5)=4 objets et est donc (9-9)(9-7)(9-5)(9-3)(9-1) = 02468 ==> 86420.
Si on s'intéresse à 441 à 3 objets:
- En considérant une hauteur maximum de 5, le Dual associé a (5-3)=2 objets et est donc (5-4)(5-4)(5-1) = 114 ==> 411.
- Si on avait choisi une hauteur maximum de 7, le Dual associé aurait eu (7-3)=4 objets et serait donc (7-4)(7-4)(7-1) = 336 ==> 633.
- Si on avait choisi une hauteur maximum de 6, le Dual associé aurait eu (6-3)=3 objets et serait donc (6-4)(6-4)(6-1) = 225 ==> 522.
Le dernier exemple est particulièrement intéressant: le Dual est différent, contient le même nombre d'objets et se retrouve en parcourant le même diagramme Etats/Transitions.
Observons donc le diagramme correspondant de 2 objets et de hauteur maximum 4.
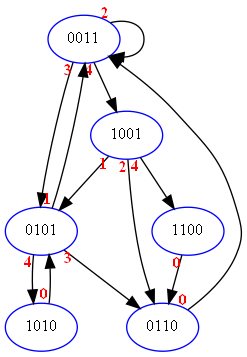
La majeur partie des Etats est leur propre dual, excepté 1001 et 0110. Si on réorganise le diagramme pour calquer ses duaux on obtient:
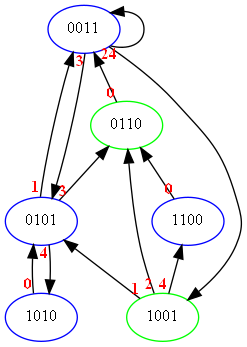
On a donc le résultat suivant:
Le résultat précédent nous dit donc que tous les Duaux associés de 2 objets et de hauteur 4 sont portés par le même Diagramme Etats/Transitions; tout comme tous les Duaux de 3 objets et de hauteur 6, de 4 objets et de hauteur 8 ...
Certains Siteswaps peuvent également être leur propre Dual en considérant une hauteur maximum de 2B. C'est le cas par exemple de 741 à 4 objets pour une hauteur de 8 ou encore 666000 à 3 objets pour une hauteur maximum de 6.
L'opération de dualité appliquée sur certains siteswaps particuliers conserve cette particularité:
- Comme indiqué par Jack Boyce au sein de The Longest Prime Siteswap Patterns, le Dual d'un Siteswap Premier donne un Siteswap Premier et en particulier le Dual d'un Siteswap Premier maximum donne un Siteswap Premier maximum.
- Le Dual d'un Siteswap Vanille Magique est un Siteswap Vanille Magique.
- Le Dual d'un Siteswap Vanille Scramblable est un Siteswap Vanille Scramblable.
- Le Dual d'un Siteswap Vanille Reversible est un Siteswap Vanille Reversible.
- Le Dual d'un Siteswap Vanille Palindrome est un Siteswap Vanille Palindrome.
Nous reviendrons sur ces différentes propriétés au sein des chapitres concernés mais si vous avez déjà connaissance de ces différents Siteswaps particuliers, vous trouverez des éléments de démonstration ici.
X-2 - Notation Multiplexe
En notation Multiplexe on peut retrouver ces Siteswaps Duaux pour un nombre Maximum de lancers par Multiplexe au sein du Siteswap. On note en effet au sein du Chapitre V-2 qu'on retouve le même nombre d'Etats et de Transitions pour une hauteur donnée et un nombre différent d'objets. Bien entendu on retrouve également cette propriété au sein des diagrammes Etats/Transitions Multiplexes réduits.
Regardons par exemple le diagramme Etats/Transitions de 2 objets, d'une hauteur maximum 3 et comportant au maximum 2 lancers par Multiplexe:
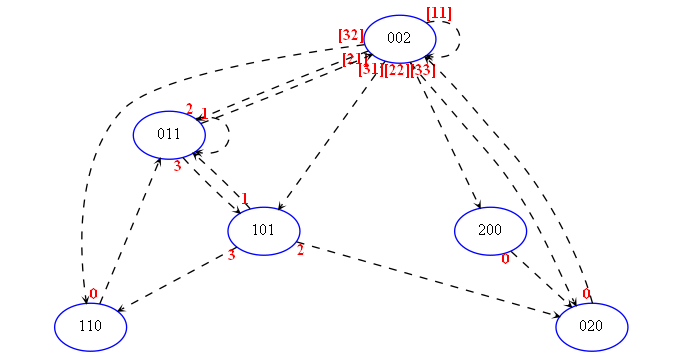
Si on essaie de calquer le diagramme Etats/Transitions de 4 objets, d'une hauteur maximum 3 et comportant au maximum 2 lancers par Multiplexe on obtient:
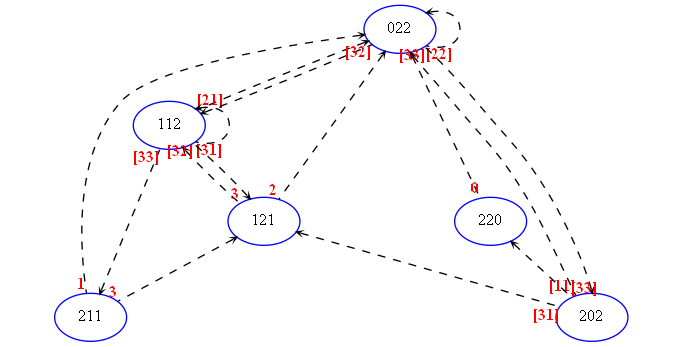
On obtient des résultats assez similaires à ceux précédemment indiqués en notation Vanille:
- Un état Dual Multiplexe se déduit en réalisant un complément à M d'un état et en inversant ce résultat. M étant le nombre maximum de lancers par Multiplexe.
- Une transition Duale pour une hauteur maximum H se déduit en inversant le sens de la transition. Pour le calcul de sa valeur, on effectue (H-Vk) pour chacun des chiffres Vk et on ajoute autant de H qu'il est nécessaire pour obtenir M chiffres.
- On va considérer chaque lancer indépendemment. On va donc encadrer chaque lancer simplex par les symboles '[' et ']' pour les représenter ainsi en Multiplexe.
- On ajoute ensuite à la fin de chaque Multiplexe autant de 0 que nécessaire afin qu'il y ait M chiffres dans chaque lancer.
- Pour chacun des chiffres Vk du Siteswap ainsi obtenu on effectue l'opération H-Vk.
- On inverse le résultat obtenu tout en le simplifiant par suppression des 0 au sein des Multiplexes et des symboles '[' et ']' si après coup il ne s'agit plus que d'un lancer simplexe.
- Le Siteswap ainsi obtenu nécessite H*M-B objets, B étant le nombre d'objets du Siteswap originel.
Prenons pour exemple 24[54], relativement connu à 5 objets. Ce Siteswaps a 2 lancers Maximums par Multiplexe.
- En considérant une hauteur maximum de 6 on obtient: [(6-2)6][(6-4)6][(6-5)(6-4)] ==> [46][26][12] ==> [21][62][64]. Il s'agit donc d'un Siteswap de (6*2-5) = 7 objets.
- En considérant une hauteur maximum de 5 on obtient: [(5-2)5][(5-4)5][(5-5)(5-4)] ==> [35][15][01] ==> 1[51][53]. Il s'agit donc d'un Siteswap de (5*2-5) = 5 objets.
Le dernier exemple montre encore que certains diagrammes Etats/Transitions peuvent porter des couples de Duaux avec des valeurs différentes.
En l'occurence on a donc le résultat suivant:
Le résultat précédent nous dit donc que tous les Duaux associés de 2 objets, de hauteur 2 avec 2 lancers maximum par Multiplexe sont portés par le même Diagramme Etats/Transitions; tout comme tous les Duaux de 3 objets, de hauteur 3 avec 2 lancers maximum par Multiplexe; de 4 objets, de hauteur 4 avec 2 lancers maximum par Multiplexe; de 3 objets, de hauteur 2 avec 3 lancers maximum par Multiplexe; de 6 objets, de hauteur 4 avec 3 lancers maximum par Multiplexe ...
L'opération de dualité appliquée sur certains Siteswaps Multipexes particuliers conserve cette particularité:
- Le Dual d'un Siteswap Multiplexe Premier donne un Siteswap Multiplexe Premier.
- Le Dual d'un Siteswap Multiplexe Reversible est un Siteswap Multiplexe Reversible.
- Le Dual d'un Siteswap Multiplexe Scramblable est un Siteswap Multiplexe Scramblable.
- Le Dual d'un Siteswap Multiplexe Palindrome est un Siteswap Multiplexe Palindrome.
- En revanche, Le Dual d'un Siteswap Multiplexe Magique n'est pas spécialement un Siteswap Multiplexe Magique.
X-3 - Notation Synchrone, Synchrone Multiplexe & MultiSynchrone
Dans ces différentes familles, au vu du nombre identique d'états pour une même hauteur maximum et un nombre différent d'objets, on sent que la notion de dualité est proche. Cependant le nombre de transitions reste distinct. C'est une conséquence directe de l'utilisation du symbole « X ». Bien qu'on puisse imaginer trouver une correspondance, il ne s'agit plus de dualité; une transition peut devenir multiple ou disparaître. Il serait cependant intéressant d'établir le lien entre ces différents triplets, quadruplets, ...
| ❮ | ❯ |



