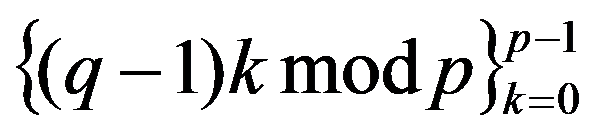Jonglage.net

La Notation Siteswap (Concepts Avancés) (11/20)

Article proposé par Frédéric Roudaut

Le 15/11/2015.

❮

❯

XI - Siteswaps Magiques

On retrouve régulièrement dans la littérature le qualificatif de séquences magiques de période P tout Siteswap Vanille qui contient une et une seule fois chacun des chiffres de 0 à P-1. On rappelle que dans le cadre de notre article la hauteur maximum à été fixée à 15 afin que celle-ci soit codable par un unique chiffre hexadécimal. La période maximum que l'on peut rencontrer ici au sein des Siteswaps Magiques est donc limitée à 15.

On peut étendre cette définition en jouant sur la parité des lancers. On a alors :

des Siteswaps Magiques Vanilles Pairs de période P : qui contiennent l'ensemble des chiffres pairs en hexadécimal de 0 à 2*(p-1);
des Siteswaps Magiques Vanilles Impairs de période P : qui contiennent l'ensemble des chiffres impairs en hexadécimal de 1 à 2*p -1;

On parlera donc de Siteswaps Magiques Sans Parité ou tout simplement Siteswaps Magiques lorsque les lancers usités ne sont pas cloisonnés aux cas pairs ou impairs.

Avec les définitions précédentes on a par exemple à 4 objets :

012345678 : Siteswap Magique de période 9;
86420 : Siteswap Magique Pair de période 5;
7531 : Siteswap Magique Impair de période 4.

Il n'y a pas de raison de cloisonner les Siteswaps Magiques aux Siteswaps Vanilles. Par la suite on donnera donc des Siteswaps Magiques pour chacune des différentes familles de Siteswaps. Le qualificatif de Période pour un Siteswap Magique n'aura plus réellement lieu d'être et on préférera lui substituer le terme de Longueur pour éviter les confusions avec la période effective des Siteswaps associés.

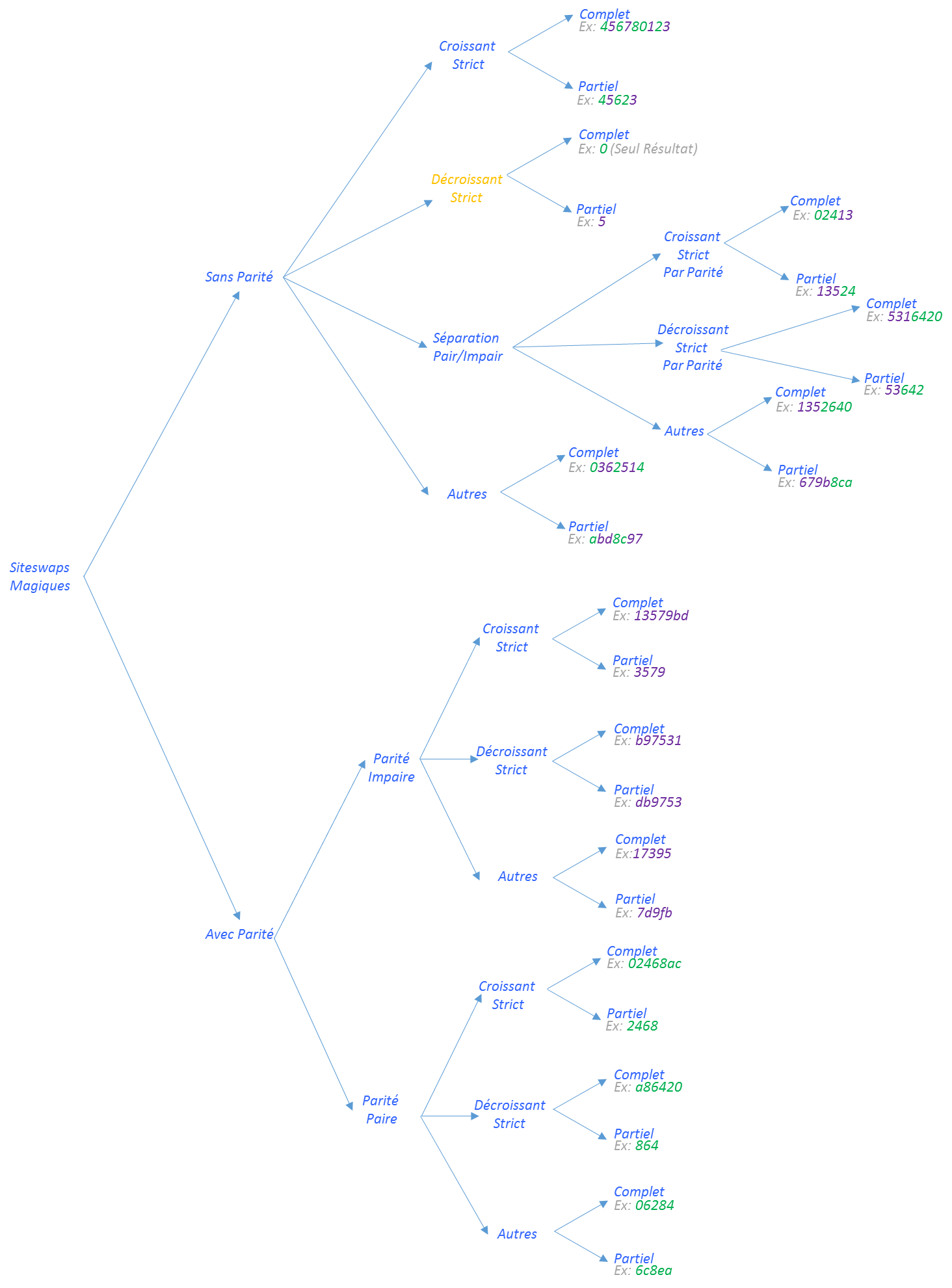
On constate qu'avec les définitions précédentes on commence la partition à chaque fois depuis le chiffre initial 0 ou 1. On peut imaginer des Siteswaps Magiques Partiels qui relâchent cette contrainte et débutent le partitionnement à une valeur supérieure. Par opposition on parlera de Siteswaps Magiques Complets (éventuellement Pairs ou Impairs) lorsque le plus petit lancer correspond à la valeur initiale de la partition.

L'arbre ci-dessous présente les différentes définitions que l'on va considérer ici:

Enfin on aurait pu également ajouter à ces familles de Siteswaps, toute progression arithmétique non prise en compte par les définitions précédentes. Une progression Arithmétique est une suite de chiffre dont la différence entre 2 chiffres consécutifs est constante. Avec nos définitions de Siteswaps Magiques, cette différence vaut 1 ou -1 (pour les Siteswaps Magiques sans Parité) et 2 ou -2 (pour les Siteswaps Magiques avec Parité). On a bien évidemment des progressions arithmétiques avec des différences de 3, 4 ... 741 est un exemple de progresssion arithmétique avec une différence de -3.

XI-1 - Algorithme de Jonathan Stadler

Burkard Postler, dans son ouvrage "The Mathematics Of Juggling" fait référence à un algorithme proposé par Jonathan Stadler en 1994 dans le forum rec.juggling pour trouver certains des Siteswaps Magiques.

Cet algorithme ne donne qu'une partie des Siteswaps Magiques Complets Sans Parité mais est relativement simple et s'appuie sur la formule suivante (avec p et q premiers entre eux) :

Pour une période p donnée, il suffit donc de choisir q dans l'intervalle [2..p-1].

Le tableau ci-dessous résume les Siteswap Magiques obtenus à l'aide de cette formule.

		Période
	SS Magiques Stadler	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1				012
	2						01234 02413 03142
	3								0123456 0246135 0362514 0415263 0531642
	4										012345678 048372615 075318642
	5												0123456789a 02468a13579 0369147a258 04815926a37 05a49382716 061728394a5 073a6295184 0852a741963 097531a8642
	6														0123456789abc 02468ac13579b 0369c258b147a 048c37b26a159 05a27c4916b38 06c5b4a392817 0718293a4b5c6 083b6194c72a5 0951a62b73c84 0a741b852c963 0b97531ca8642
	7																0123456789abcde 07e6d5c4b3a2918 0db97531eca8642
	8
	9
	10
	11
	12
	13
	14
	15

Un choix de q relativement intéressant est p-1 : il sépare les lancers impairs des lancers pairs. Si on choisit par exemple p=7, on obtient ainsi le Siteswap à 3 objets 0531642. Si on choisit p=11 on obtient le Siteswap intéressant à 5 objets 097531a8642.

Jonathan Stadler montre également que ces Siteswaps Magiques Complets sont obligatoirement de période impaire.

XI-2 - Enumération des Siteswaps Magiques Complets

a - Notation Vanille

Le tableau ci-dessous présente les Siteswaps Magiques Complets Pair en jaune, Impair en vert et Sans Parité en Rose. Les cases plus foncées ne sont pas considérées, les lancers nécessaires dépassant notre limite de hauteur de lancer fixée à la valeur hexadécimale f. Pour une meilleur visibilité, les équivalences par permutation ont été supprimées.

Ce tableau montre clairement que l'Algorithme de Stadler ne donne qu'un sous-ensemble des Siteswaps Vanilles Magiques Complets Sans Parité.

		Période
	SS Magiques Complets Vanilles	0	1	2	3	4	5	6	7	8	9	10
Nombre d'objets	0		0
	1		1	20	120
	2			31	420		23401 24130 31420
	3				531	* 0246 * 6420			3456012 3461520 3526401 3562041 3625140 3641502 4256130 4263501 4516302 4612530 4613502 4630512 5246031 5261340 5263041 5316420 5360241 6235041 6314502
	4					1357 7531	* 02468 * * 06284 * 86420				225 Siteswaps
	5						* 13579 * * 17395 * 97531	* 0284a6 * * 028a46 * * 0426a8 * * 0486a2 * * 06284a * * 0628a4 * * 06824a * * 0682a4 * * 0824a6 * * 082a46 * * 0a2648 * a86420
	6							* 1395b7 * * 139b57 * * 1537b9 * * 1597b3 * * 17395b * * 1739b5 * * 17935b * * 1793b5 * * 1935b7 * * 193b57 * * 1b3759 * b97531	* 02468ac * * 0248ca6 * * 024c86a * * 026a84c * * 02a648c * * 042c68a * * 04682ca * * 04862ac * * 048ac62 * * 048c26a * * 082a4c6 * * 08426ac * * 08ac264 * * 0a468c2 * * 0a62c84 * * 0a8c246 * * 0c268a4 * * 0c8246a * ca86420
	7								* 13579bd * * 1359db7 * * 135d97b * * 137b95d * * 13b759d * * 153d79b * * 15793db * * 15973bd * * 159bd73 * * 159d37b * * 193b5d7 * * 19537bd * * 19bd375 * * 1b579d3 * * 1b73d95 * * 1b9d357 * * 1d379b5 * * 1d9357b * db97531	144 Siteswaps
	8									144 Siteswaps
	9
	10
	11
	12
	13
	14
	15

b - Notation Multiplexe

c - Notation Synchrone

		Période
	SS Magiques Complets Synchrones	0	1	2	3	4	5	6	7	8	9	10
Nombre d'objets	0
	1			(0,2)
	2
	3					* (0,6)(2x,4x) * * (0,6)(4,2) * * (0,6x)(2x,4) * * (0,6x)(4x,2) * (4,6)(0,2) (4,6x)(2x,0) (4x,6)(0,2x) (4x,6x)(2,0)
	4
	5							144 Siteswaps
	6
	7
	8
	9
	10
	11
	12
	13
	14
	15

d - Notation Synchrone Multiplexe

e - Notation Multisynchrone

XI-3 - Enumération des Siteswaps Magiques Partiels Vanilles

On rappelle qu'un Siteswap Complet de période P est un Siteswap qui contient une et une seule fois chacun des chiffres de 0 à P-1. On a également défini des Siteswaps Magiques Complets pairs, contenant uniquement des lancers pairs et bien entendu des Siteswaps Magiques Complets impairs constitués uniquement de lancers impairs.

Dans le cas des Siteswaps Magiques Partiels le partionnement débute à une valeur supérieure à 0. On a donc également des Siteswaps Magiques Partiels pairs, impairs et sans parité (ie qui contiennent l'ensemble des chiffres du partionnement). Nous n'allons pas énumérer pour chaque famille les différents Siteswaps Magiques Partiels mais ceux qui sont intéressés par ceux relatifs aux Siteswaps Vanilles, les trouveront en intégralité en cliquant sur les liens des tableaux ci-dessous, pour un partionnement depuis la valeur 1 jusqu'à la valeur 15.

Les cases des tableaux comportant uniquement des Siteswaps Magiques Partiels Pairs sont colorisées en jaune; celles comportant uniquement des Siteswaps Magiques Partiels Impairs sont en vert; celles comportant uniquement des Siteswaps Magiques sans Parité sont en rose. Certaines cases sont blanches dans la mesure où parfois les Siteswaps sans Parité sont également Pairs ou Impairs. En fait dans le cas où le partionnement débute à une valeur impaire, ceux-ci sont également Impairs et inversement.

		Période
	Nombre SS Magiques Partiels Vanilles Start = 6	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6		1
	7		1	1	1
	8			1	1		3
	9				1	2			19
	10					2	3				225
	11						3
	12
	13
	14
	15

		Période
	Nombre SS Magiques Partiels Vanilles Start = 7	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7		1
	8		1	1	1
	9			1	1		3
	10				1	2			19
	11					2	3				225
	12
	13
	14
	15

		Période
	Nombre SS Magiques Partiels Vanilles Start = 8	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7
	8		1
	9		1	1	1
	10			1	1		3
	11				1	2			19
	12					2
	13
	14
	15

		Période
	Nombre SS Magiques Partiels Vanilles Start = 9	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7
	8
	9		1
	10		1	1	1
	11			1	1		3
	12				1	2			19
	13
	14
	15

		Période
	Nombre SS Magiques Partiels Vanilles Start = a	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7
	8
	9
	10		1
	11		1	1	1
	12			1	1		3
	13				1
	14
	15

		Période
	Nombre SS Magiques Partiels Vanilles Start = b	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7
	8
	9
	10
	11		1
	12		1	1	1
	13			1	1		3
	14
	15

		Période
	Nombre SS Magiques Partiels Vanilles Start = c	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7
	8
	9
	10
	11
	12		1
	13		1	1	1
	14			1
	15

		Période
	Nombre SS Magiques Partiels Vanilles Start = d	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7
	8
	9
	10
	11
	12
	13		1
	14		1	1	1
	15

		Période
	Nombre SS Magiques Partiels Vanilles Start = e	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7
	8
	9
	10
	11
	12
	13
	14		1
	15		1

		Période
	Nombre SS Magiques Partiels Vanilles Start = f	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0
	1
	2
	3
	4
	5
	6
	7
	8
	9
	10
	11
	12
	13
	14
	15		1

XI-4 - Siteswaps Magiques Vanilles croissants/décroissants stricts

Lors des énumérations précédentes des Siteswaps Magiques Vanilles Partiels ou Complets, vous avez pu noter que pour certains de ces Siteswaps au delta de leur rotation, les chiffres de ceux-ci étaient ordonnés selon un ordre strictement croissant ou décroissant. L'idée de ce chapitre est simplement de faire ressortir ces différents Siteswaps remarquables.

a - Siteswaps Magiques sans Parité

Les tableaux ci-dessous donnent les Siteswaps Magiques Partiels/Complets strictement croissants/décroissants sans considération de parité. Les Siteswaps ci-dessous sont donnés de préférence sous leur format fondamentaux et on notera qu'il est ici possible pour chacun d'entre-eux d'en dégager un tel format. Pour un nombre d'objets donné, vous pourrez donc vous amuser à les enchaîner sans transition. On notera qu'il n'y a pas de Siteswaps Magiques strictement décroissants; sauf les figures de base (ie 3, 4, 5 ...) qui sont bien entendu à la fois croissantes et décroissantes.

		Période
	SS Magiques Vanilles Croissants Sans Parité	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0		0
	1		1		120
	2		2		231		23401
	3		3		342		34512		3456012
	4		4		453		45623		4567123		456780123
	5		5		564		56734		5678234		567891234		56789a01234
	6		6		675		67845		6789345		6789a2345		6789ab12345		6789abc012345
	7		7		786		78956		789a456		789ab3456		789abc23456		789abcd123456		789abcde0123456
	8		8		897		89a67		89ab567		89abc4567		89abcd34567		89abcde234567		89abcdef1234567
	9		9		9a8		9ab78		9abc678		9abcd5678		9abcde45678		9abcdef345678
	10		a		ab9		abc89		abcd789		abcde6789		abcdef56789
	11		b		bca		bcd9a		bcde89a		bcdef789a
	12		c		cdb		cdeab		cdef9ab
	13		d		dec		defbc
	14		e		efd
	15		f

		Période
	SS Magiques Vanilles Décroissants Sans Parité	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0		0
	1		1
	2		2
	3		3
	4		4
	5		5
	6		6
	7		7
	8		8
	9		9
	10		a
	11		b
	12		c
	13		d
	14		e
	15		f

b - Siteswaps Magiques avec Parité

Les tableaux ci-dessous donnent les Siteswaps Magiques Partiels/Complets strictement croissants/décroissants avec à présent considération de la parité. Les Siteswaps comportant uniquement des lancers pairs sont colorisés en jaune; ceux comportant uniquement des lancers impairs sont en vert. On retrouve bien évidemment parmi les Siteswaps strictement croissants et décroissants ceux comportant un seul lancer et 2 lancers. Encore une fois on a cherché à écrire les Siteswaps de préférence sous leur format fondamentaux. On notera qu'il est ici possible dans le cas décroissant d'en dégager un tel format contrairement au cas croissant où c'est seulement possible pour les cas qu'on retrouve dans les cas décroissants. Pour un nombre d'objet donné, vous pourrez donc vous amuser à enchaîner les Siteswaps Magiques avec parité, décroissants, sans transition.

		Période
	SS Magiques Vanilles Croissants Avec Parité	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0		0
	1		1	20
	2		2	31
	3		3	42		* 0246 *
	4		4	53		* 1357 *	* 02468 *
	5		5	64		* 2468 *	* 13579 *
	6		6	75		* 3579 *	* 2468a *		* 02468ac *
	7		7	86		* 468a *	* 3579b *		* 13579bd *	* 02468ace *
	8		8	97		* 579b *	* 468ac *		* 2468ace *	* 13579bdf *
	9		9	a8		* 68ac *	* 579bd *		* 3579bdf *
	10		a	b9		* 79bd *	* 68ace *
	11		b	ca		* 8ace *	* 79bdf *
	12		c	db		* 9bdf *
	13		d	ec
	14		e	fd
	15		f

		Période
	SS Magiques Vanilles Décroissants Avec Parité	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0		0
	1		1	20
	2		2	31	420
	3		3	42	531	6420
	4		4	53	642	7531	86420
	5		5	64	753	8642	97531	a86420
	6		6	75	864	9753	a8642	b97531	ca86420
	7		7	86	975	a864	b9753	ca8642	db97531	eca86420
	8		8	97	a86	b975	ca864	db9753	eca8642	fdb97531
	9		9	a8	b97	ca86	db975	eca864	fdb9753
	10		a	b9	ca8	db97	eca86	fdb975
	11		b	ca	db9	eca8	fdb97
	12		c	db	eca	fdb9
	13		d	ec	fdb
	14		e	fd
	15		f

c - Siteswaps Magiques sans Parité et séparation lancers pairs/impairs

On peut également dégager d'autres Siteswaps Magiques Partiels/Complets avec Parité qui séparent complètement les lancers pairs des lancers impairs; chacune des sections utilisant un ordre strictement Croissant/Décroissant. Les tableaux ci-dessous résument ces différents Siteswaps Magiques :

		Période
	SS Magiques Vanilles Croissants Sans Parité, Séparation Pair/Impair	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0		0
	1		1
	2		2				24130
	3		3				35241		4613502
	4		4				46352		5724613
	5		5				57463		6835724				* 68a13579024 *
	6		6				68574		7946835				* 79b2468a135 *		* 8ac13579b0246 *
	7		7				79685		8a57946				* 8ac3579b246 *		* 9bd2468ac1357 *
	8		8				8a796		9b68a57				* 9bd468ac357 *		* ace3579bd2468 *
	9		9				9b8a7		ac79b68				* ace579bd468 *		* bdf468ace3579 *
	10		a				ac9b8		bd8ac79				* bdf68ace579 *
	11		b				bdac9		ce9bd8a
	12		c				cebda		dface9b
	13		d				dfceb
	14		e
	15		f

		Période
	SS Magiques Vanilles Décroissants Sans Parité, Séparation Pair/Impair	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Nombre d'objets	0		0
	1		1		120
	2		2		231		31420
	3		3		342		42531		5316420
	4		4		453		53642		6427531		753186420
	5		5		564		64753		7538642		864297531		97531a86420
	6		6		675		75864		8649753		9753a8642		a8642b97531		b97531ca86420
	7		7		786		86975		975a864		a864b9753		b9753ca8642		ca8642db97531		db97531eca86420
	8		8		897		97a86		a86b975		b975ca864		ca864db9753		db9753eca8642		eca8642fdb97531
	9		9		9a8		a8b97		b97ca86		ca86db975		db975eca864		eca864fdb9753
	10		a		ab9		b9ca8		ca8db97		db97eca86		eca86fdb975
	11		b		bca		cadb9		db9eca8		eca8fdb97
	12		c		cdb		dbeca		ecafdb9
	13		d		dec		ecfdb
	14		e		efd
	15		f

On remarquera que dans le cas strictement croissant, certains des Siteswaps précédents sont fondamentaux, alors que les Siteswaps Magiques avec Parité strictement croissants ne l'étaient pas. L'ajout de la parité opposée nous donne donc dans certains cas une transition intéressante pour amorcer ces Siteswaps avec Parité strictement croissants.

❮

❯

Contact |

SiteSwap1 (SS1):
SiteSwap2 (SS2):

Transitions de SS1 vers SS2		Transitions de SS2 vers SS1
Longueur :		Longueur :
Lancer max :		Lancer max :

Séquence :
Lancers/sec :		Vélocité :		Couleur :