Ladder Notation : Notation en Echelle (1/8)
Article proposé par Frédéric Roudaut
Le 23/04/2012.
Corrections : Le 25/03/2015.
La Ladder Notation ou Notation en Echelle est une notation graphique créée dans les années 80, revendiquée par Charlie Dancey qui avoue s'être inspiré de notations similaires déjà existantes. Cet article a pour ambition de vous faire appréhender cette notation fort simple mais tellement puissante. On cherchera de plus à montrer l'adéquation de cette représentation avec la notation Siteswap.
III - PORTEE DE LA MODELISATION
IV - ANALOGIE AVEC LES VALEURS DES LANCERS EN SITESWAP
V-1 - Siteswaps Asynchrones Basiques
V-2 - Autres Siteswaps Asynchrones
VI-1 - Figures de même synchronisation
VI-2 - Transitions Synchrone/Asynchrone
VI-3 - Exemples de transitions entre synchronisations distinctes
VIII - DROP(S) & ADDITION(S) D'OBJETS
IX-1 - Déplacement Droite/Gauche des mains
IX-2 - Prise en compte du Rebond
IX-3 - Position des bras et trajectoire des objets (MMSTD & SOU)
IX-4 - Trajectoires autour du corps (BTN)
- 423, 4 en Shoulder Throw (4<alac> 2 3)
- Backcross 3 Objets (3<alopac>)
- Exemple de Bodytricks 3 Objets
X - TRANSFORMATIONS DES DIAGRAMMES & NOUVELLES FIGURES
X-1 - Superposition et décomposition de diagrammes
- [64][62]1[22]2 = 66120 + 42022
- ([44],[44])(4x,0)* = (4,4)(4x,0)* + (4,4)(0,0)*
X-3 - Décalage des Beats d'une main
X-4 - Diagrammes Time-Reversed
X-5 - Modifications du Dwell Time, de l'Airtime, du Dwell Ratio ...
| ❯ |
I - INTRODUCTION
Comme indiqué en présentation de cet article, il semblerait qu'il faille attribuer la définition de ces diagrammes en échelle à Charlie Dancey dans les années 80 (84 selon lui-même). Cette notation est d'ailleurs très présente aux seins de ses 2 livres : Encyclopædia of Ball Juggling et Compendium of Club Juggling. Cependant publié uniquement en 1993/1994, on trouve dans la littérature des diagrammes équivalents dans les années antérieures et il reste difficile de savoir qui est véritablement le premier à les avoir découvert; d'autant plus que Simpson en publie un exemple en 1986 dans Juggler's World, Vol37-No.4,p31 Vous obtiendrez des précisions complémentaires dans les articles de Arthur Lewbel, The Invention of Juggling Notations, 1993-1994 ainsi que la version issue de Juggler's World, 1997,Vol49-No.2,p57. Des diagrammes similaires ont probablement été découverts et redécouverts de manière totalement indépendantes par différents jongleurs dans les années 80.
Ci-dessous vous aurez un aperçu de quelques-uns de ces diagrammes publiés dans les années 80-90.
 Storer, 1978 |
||
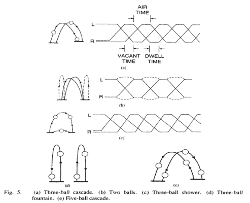 Shannon, 1981 |
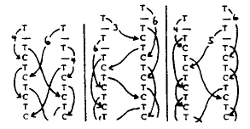 Walker, 1982 |
|
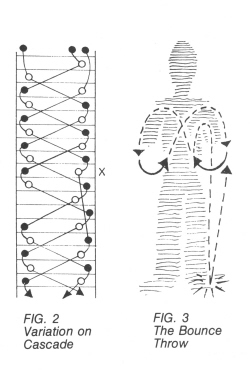 Simpson, 1986 |
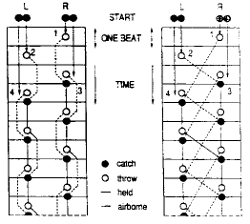 Beek, 1989 |
|
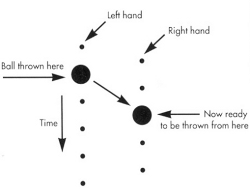 Tiemann & Magnusson, 1991 |
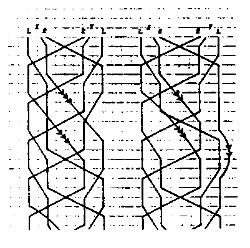 Voigt, 1992 |
|
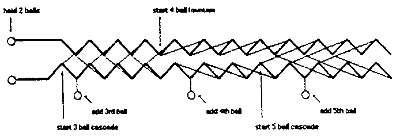 Kalvan, 1992 |
||
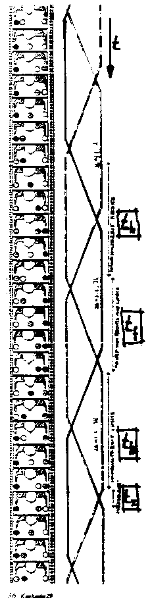 Jota, 1993 |
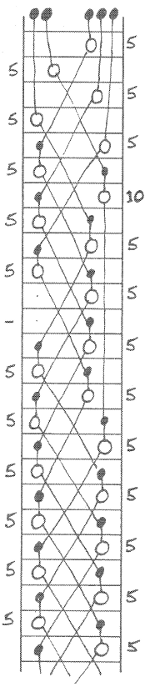 Dancey, 1994 |
|
Si vous cherchez des informations complémentaires sur ces diagrammes, vous pourrez consulter les articles de :
- Dave Storer : A Written Notation For Describing Ball Juggling Tricks, IJA Newsletter, 1978, Vol30-No.2,p7
- Claude Shannon : Scientific Aspects of Juggling, 1981
- Jeff Walker : Variations for numbers jugglers, Juggler's World, 1982, Vol34-No.1,p11
- Charlie Simpson : Juggling on paper, Juggler's World, 1986, Vol37-No.4,p31
- Bruce Tiemann and Bengt Magnusson : A Notation for Juggling Tricks. A LOT of Juggling Tricks, Juggler's World, 1991, Vol43-No.2,p31
Bien qu'il n'est pas indispensable de connaître la Notation Siteswap pour appréhender les concepts de la Ladder Notation, je ne peux que vous conseiller d'en connaître les bases avant de poursuivre plus avant la lecture de cet article. Je ferais en effet référence aux figures sous leur format Siteswap souvent bien connu tout en montrant l'adéquation des 2 notations et le passage de l'une à l'autre. Vous pourrez donc vous reporter à l'article Introduction à la notation Siteswap au besoin.
D'autre part j'utiliserais la Notation Siteswap telle qu'elle est utilisée et définie par JugglingLab; de nombreux exemples seront d'ailleurs illustrés à partir de cet outil. La version utilisée sera la v0.6.1 (Octobre 2011). Ceux qui utilisent JoePass ou un autre simulateur adapteront au besoin les éventuelles différences.
Si au cours de la lecture de cet article certaines figures vous paraissent trop petites, clickez dessus pour obtenir une vue plus grande.
II - L'ECHELLE DE TEMPS
La Ladder Notation est une notation entièrement graphique qui comme son nom l'indique repose sur une échelle de temps. A chaque barreau de l'échelle correspondra un Événement de jonglerie. Cet événement peut-être un lancer, une récupération, ou encore une attente avec ou sans objet en main. En anglais le terme utilisé est Beat (battement, pulsation). Je conserverais le terme anglais pour éviter les ambiguïtés éventuelles par la suite.
Cette échelle est généralement dessinée verticalement de haut en bas (Choix de Dancey) mais on peut tout aussi bien la dessiner horizontalement de gauche à droite. C'est le choix que je ferais par la suite par pur souci d'occupation de l'espace de cette page. On notera d'ailleurs qu'en physique ou en mathématiques, par convention, les axes de temps sont notés de gauche à droite.
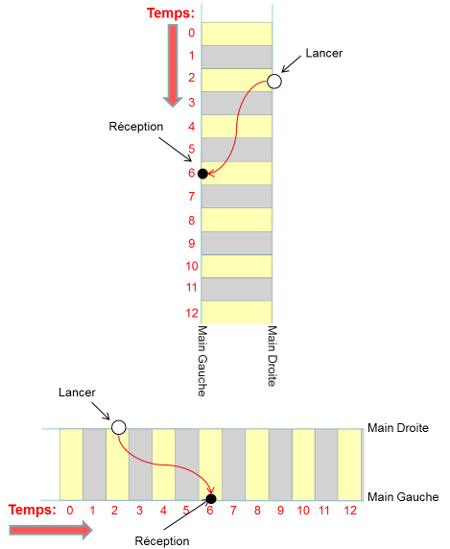
Sur une échelle horizontale le montant droit correspondra à la main droite, le gauche à la main gauche. Par simple rotation de 90° dans le sens trigonométrique, sur une échelle verticale la main droite correspondra donc au montant supérieur tandis que la gauche sera le montant inférieur. On portera sur cette échelle les différents objets modélisés par des balles. On fera ainsi correspondre à un lancer un grand disque blanc et à une récupération un petit disque noir. Un lien modélisant le trajet sera établi entre le lancer et la récupération associée. La figure ci-dessous présente ces divers éléments sur les 2 positionnements principaux de l'échelle.
Ces diagrammes en échelle nous donnent une représentation du jongleur par-dessus. On comprend que Charlie Dancey ait décidé de modéliser avec son échelle verticale la main droite par le barreau droit, la main gauche par le barreau gauche. D'autant plus qu'en notation Siteswap Synchrone, la main gauche est indiquée en premier également. Mais étant donné que le temps croît de haut en bas, on aurait pu imaginer le contraire. Ceci aurait finalement été aussi judicieux pour modéliser un jongleur se déplaçant selon l'axe des temps. Son observation par-dessus nous montrerait donc la trajectoire des balles de manière similaire à la Ladder Notation. Charlie Dancey en fait pourtant une analogie avec un skatteur avançant sur l'échelle selon l'axe des temps et jonglant avec des balles lumineuses.
III - PORTEE DE LA MODELISATION
Avant de poursuivre il est bon de se rappeler que le rythme des lancers nous impose 2 grandes familles de figures :
- les figures asynchrones : chaque main lance successivement l'une après l'autre. Dans la forme simple il n'est pas possible de récupérer plusieurs objets dans la même main au même moment.
- les figures synchrones : les mains lancent en même temps (ou rien si elle n'ont pas d'objets). Dans la forme simple il n'est pas possible de récupérer plusieurs objets dans la même main au même moment.
Je parlerais de Synchronisation de la figure, n'ayant pas trouvé de terme plus adéquat.
Pour chacune de ses familles il est possible d'alléger les contraintes et d'autoriser les lancers multiples et les réceptions simultanées. On a donc également des figures asynchrones multiplexes ainsi que des figures synchrones multiplexes.
Il est même éventuellement possible d'affiner encore cette classification dès lors que l'on a des multiplexes. Il en effet très délicat de récupérer de manière simultanées plusieurs objets dès lors que plus d'un lancer du multiplexe est différent du Siteswap 2. Cette classe de figure peut donc également être dissociée.
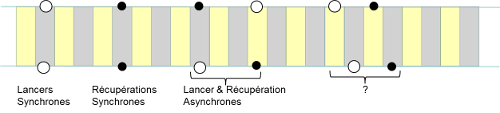
La Ladder Notation permet d'adresser toutes ces différentes figures sans exception. Un lancer Synchrone correspond tout simplement à 2 disques blancs sur le même Beat, pour une récupération Synchrone il s'agit de 2 petits disques noirs ... La figure ci-dessous modélise ces divers rythmes.
On remarquera les 2 cas particuliers dont une main est vide (l'autre lance ou récupère). Pris isolément il n'est pas possible de conclure s'il s'agit d'un lancer Asynchrone/Synchrone. La dominance éventuelle de la Figure permet de définir le rythme du lancer. Le cas échéant on peut considérer les 2 types de lancer/récupération.
Avec une telle notation, dans le cas d'un rythme de même synchronisation, chaque main lancera un objet au minimum tous les 2 Beats. Cependant dans le cas d'une figure synchrone un objet n'est lancé que tous les 2 Beats tandis que dans le cas d'une figure asynchrone un objet est éventuellement lancé à chaque Beat.
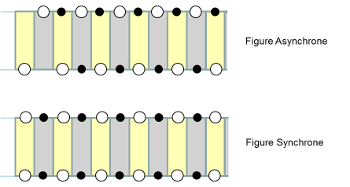
On remarquera que rien n'interdit cependant de faire cohabiter lancers Synchrones et Asynchrones. On comprend donc rapidement qu'il s'agit ici d'un outil intéressant pour trouver des transitions entre Siteswaps Asynchrones et Synchrones.
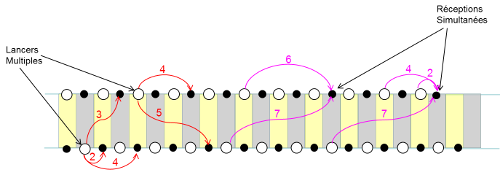
Ce type de diagramme permet également de relever aisément les lancers multiples (Multiplexes) ou les réceptions simultanées (nommées Squeeze) comme vous le constaterez dans le schéma ci-dessous :
IV - ANALOGIE AVEC LES VALEURS DES LANCERS EN SITESWAP
Il est important ici de rappeler 3 définitions importantes que sont :
- le Dwell Time : Temps pendant lequel lequel est retenu en main avant d'être relancé;
- l'Airtime (ou Flight Time) : Temps de parcours de l'objet;
- l'Empty Time (ou Vacant Time) : Temps pendant lequel la main est vide entre un lancer et la prochaine réception.
En notation Siteswap le Dwell Time est nul, les objets sont relancés dès leur récupération. Il en est de même pour l'Empty Time. En Ladder Notation, Dwell Time et Airtime valent classiquement aux alentours de 1 Beat mais il reste possible de les faire varier de manière similaire sur l'ensemble de la figure (On parlera de jonglage Uniforme) ou sur des portions uniquement rompant le caractère Uniforme du jonglage.
Le fait de jouer sur ces différents paramètres modifie parfois complètement la figure perçue (cf X-5). En Ladder Notation contrairement à la théorie du Siteswap, le Dwell Time n'est donc pas nul.
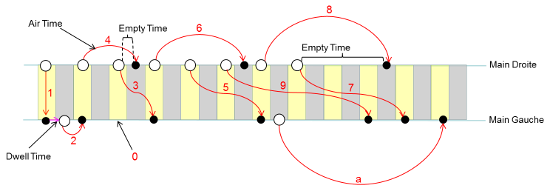
Si l'on fait une analogie avec les valeurs des lancers des Siteswaps Asynchrones (Multiplexes ou non), le nombre de Beats d'un lancer donné correspond à la valeur du Siteswap -1. Vous le constaterez dans le schéma ci-dessous. Cette différence est liée à la considération ici du Dwell Time après récupération qui ajoute approximativement 1 Temps. En notation Siteswap on a l'habitude de compter en hexadécimal ([0..9a...f]).
En notation Siteswap on ne trouve classiquement pas de chiffre impair au sein des figures Synchrones, ce qui est relativement logique puisque comme indiqué précédemment chaque main lance tous les 2 temps. Lorsque l'objet doit changer de côté on ajoute un 'x' au Siteswap. En Ladder Notation le nombre de Beats d'un lancer sera donc également la valeur du Siteswap -1. La main de récupération est l'opposée de la main du lancer si le Siteswap avait un 'x'. On note donc des lancers pair en Ladder Notation identiques au cas asynchrone.
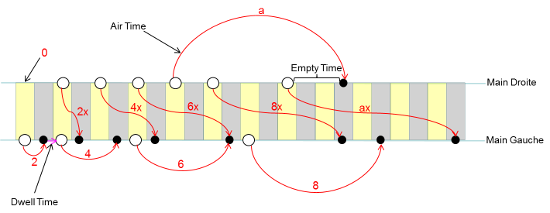
On note donc toute la cohérence de la Notation qui définit une règle similaire pour trouver la valeur Siteswap équivalente d'un lancer dans les cas Synchrones et Asynchrones.
----------------
Valeur du Lancer en Siteswap = Nombre de Beats +1
Cas Synchrone :
---------------
Si lancer croisé :
Valeur du Lancer en Siteswap = (Nombre de Beats +1) + 'X'
Sinon :
Valeur du Lancer en Siteswap = Nombre de Beats +1
L'opération inverse est donc :
S'il s'agit d'un lancer pair, la récupération se fait dans la même main sauf pour les lancers synchrones avec un 'x'
S'il s'agit d'un lancer impair, la récupération se fait dans la main opposée.
Par souci de clarté on peut ajouter les valeurs Siteswaps correspondantes au niveau des différents lancers mais il n'y a aucune obligation, la notation se suffit à elle-même sur cet aspect.
| ❯ |